数字电路基础(3)——逻辑运算

· 2023-06-07 · # 嵌入式-硬件开发-数字集成电路-数字逻辑

上一节我们教识数了，这一节我们怎么也得来个1+1吧？

别慌，这一节我们不是给你讲二进制的1b+1b=10b这种东西，这个你上节就能自己悟出来了，这里炒现饭的话就太无聊了，我这里要说的是如果你是麦兜，你要买粗面，必须还得加鱼丸，老板却告诉你有粗面没有鱼丸，你要不要买的问题。

几种基本逻辑运算

上面麦兜的答案，你是不是一下子就知道买不了，这就是生活中最简单的一种逻辑运算，你肯定还碰到下面这几种场景：

上面这三种场景，对应的就是与运算，A和B必须同时成立才为真，否则为假；或运算，只要A或者B只成立一个即可；非运算，只要A不为真就行。教科书上，喜欢给各种东西用符号来表示并发明一个运算式表示，所以上面的三种运算，书上写的运算是这样的：

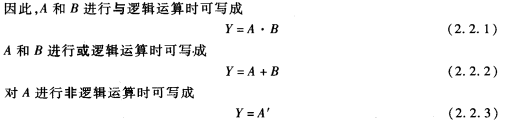
而我,是一个程序员,C语言中，这三种逻辑运算的写法是这样的：

Y = A && B  // 与
Y = A || B  // 或
Y = !A      // 非

emm，只能说各有各的剧本，各有各的唱法吧。不过作为硬件工程师，还有下面的电路图描述方法，后面我们在单片机的内部框图中，将海量的见到它们：

当然，他们仨只是最基本的三种逻辑符号，我们还可以灵活组合他们，就形成了更多更复杂的门电路，例如：与非门、或非门、异或门、同或门

与非门就是与门后面再叠加一个非门，在逻辑上也就是他们俩的叠加，先与然后取反。或非门同理。重点说的是XOR异或门和XNOR同或门。异或是指两个输入相同时，输出为0，两个不一样时，输出为1，所以叫“异”或，同或则恰好相反，相同的是1，不相同的是0，所以英文名中也加了个N，变成XNOR。

教科书上，逻辑公式列了十八种，其中有几个我认为是常识，大家靠猜可以理解出来我就不写了，我写几种写代码或者设计电路时常见的公式如下：

利用这些基本公式，可以推出下面的常用公式，这部分公式可以把复杂的式子化简，减少我们代码和电路的设计工作量，是一种化繁为简的好东西：

这些公式，我也不知道如何简洁的描述并记忆它们，理解上，如果将A和B分别换成鱼丸和粗面，也是很容易理解的。更多的时候，我在使用这些东西时，也是靠着自己的常识和理解去化简逻辑算式，好在平时并没有碰到很长的公式去化简。

算式中的A和B，可以用任何东西替换，逻辑都是成立的，可以用C替代，也可以用一个式子例如（C || D && E）替代。
逻辑运算中，将等式左右所有的东西都取反，式子还是成立的。A换!A,B换!B，||换&&，&&换||，例如Y = A && B可以转换为!Y = !A || !B

这个例子的理解和记忆，也是靠多写代码，多碰到需要逻辑判断的情况，熟能生巧吧。

逻辑运算式有公式法化简、卡诺图法化简、Q-M法化简，这三种我也没办法一下很浅显的弄懂，个人认为最后一种是可以使用代码实现的，化简思路清晰，有步骤可循，需要研究的同学自己参考下相关的资料吧，这里不做赘述。

下一章《数字电路基础(4)——逻辑门电路》，我们由抽象走向具体，开始看看我们这些逻辑在电路上的具体实现载体——门电路，看看实际上看得见摸得着的逻辑门是什么样子的。